1、基期作为考试的常考点,判断标准是问过去的时间或者“比”字后的内容,我们称之为基期,它往往和其它知识点结合在一起,例如基期比重,基期平均数,基期倍数等。那首先来看一下,基础的基期量如何来计算
基期量的计算公式,基期量=![]()
【例】1979年全国普通高校毕业生人数为8.5万人,1980年为14.7万人,2001年为114万人,2002年为145万人,2010年较上一年同比增长3.4%,2018年首次突破了800万人,2019年预计达到834万人,毕业生就业创业面临严峻形势。
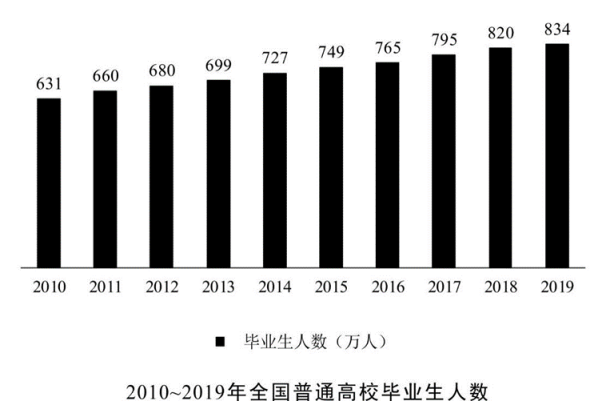
2009年全国普通高校毕业生人数约为( )。
A. 600万人
B. 610万人
C. 620万人
D. 630万人
【答案】B
【解析】
第一步,本题考查基期量计算问题。
第二步,定位柱状图与文字材料“2010年全国普通高校毕业生631万人,2010年较上一年增长3.4%”。
第三步,根据基期量=![]() ,3.4%<5%,利用化除为乘公式法,则2009年毕业生人数约为631×(1-3.4%)=631-631×3.4%≈631-21=610(万人)。
,3.4%<5%,利用化除为乘公式法,则2009年毕业生人数约为631×(1-3.4%)=631-631×3.4%≈631-21=610(万人)。
因此,选择B选项
历年考试中,单纯来考基期量相对较少,也较为简单容易得分,往往会和倍数等结合考察,关键在于截位直除和化除为乘的运用。考试中不仅会考基期量的计算,也会考察基期量的比较。
2.基期量的比较,由于基期量的公式是分数形式,因此基期量的比较一般采取分数性质和直除的方式。
【例】2019年农民工月均收入约4000元,其中外出农民工月均收入4427元,比上年增加320元;本地农民工月均收入3500元,比上年增加160元。分区域看,在东部地区就业的农民工月均收入4222元,比上年增长6.8%;在中部地区就业的农民工月均收入3794元,比上年增长6.3%;在西部地区就业的农民工月均收入3723元,比上年增长5.7%;在东北地区就业的农民工月均收入3469元,同比增长5.2%。
2018年,我国农民工在各区域的月均收入从高到低是:
A.西部地区>中部地区>东北地区>东部地区
B.中部地区>东部地区>东北地区>西部地区
C.东部地区>西部地区>东北地区>中部地区
D.东部地区>中部地区>西部地区>东北地区
【答案】D
【解析】
第一步,本题考查基期量比较。
第二步,定位文字材料第二段。
第三步,根据基期量=![]() ,可得2018年我国农民工在各区域的月均收入分别为:东部地区
,可得2018年我国农民工在各区域的月均收入分别为:东部地区![]() ,中部地区
,中部地区![]() ,西部地区
,西部地区![]() ,东北地区
,东北地区![]() ,四个分数之间分母相差不大,东部地区分子明显大于其他地区,排除A、B选项;中部地区和东北地区,直除首两位分别商35和32,中部地区>东北地区,排除C选项。
,四个分数之间分母相差不大,东部地区分子明显大于其他地区,排除A、B选项;中部地区和东北地区,直除首两位分别商35和32,中部地区>东北地区,排除C选项。
因此,选择D选项。
3.基期比重,是求过去时间的比重问题,题干中出现“占“等关键词,问的是过去的时间,常考的是在给出部分量和增长率,整体量和增长率的基础上进行计算去年的比重,相较于分别计算部分的基期量和整体的基期量,我们进一步转化成了更适合考试计算的公式,在考试中计算也有两种简便算法,一种是通过算左半部分现期比重值,再将右半部分与1进行比较,进而判断最终值较现期量的大小关系,根据选项选择;另一种是将右半部分拆一进行计算。
基期比重公式:基期比重=![]()
【例】2018年我国全年研究与试验发展(R&D)经费支出19657亿元,比上年增长11.6%,与国内生产总值之比为2.18%,其中基础研究经费1118亿元。全年境内外专利申请432.3万件,比上年增长16.9%;授予专利权244.7万件,增长33.3%;PCT专利申请受理量为5.5万件。截至年底,有效专利838.1万件,其中境内有效发明专利160.2万件,每万人口发明专利拥有量11.5件。
2017年专利授予件数占境内外专利申请件数的百分比是:
A. 47.4%
B. 49.6%
C. 50.3%
D. 56.6%
【答案】B
【解析】
第一步,本题考查基期比重计算。
第二步,定位文字材料“2018年全年境内外专利申请432.3万件,比上年增长16.9%;授予专利权244.7万件,增长33.3%”。
第三步,根据基期比重=![]() ,选项出现了首位相同第二位不同的情况,分母从左向右截取前三位并使用拆1法,即
,选项出现了首位相同第二位不同的情况,分母从左向右截取前三位并使用拆1法,即![]() ≈
≈![]() ,B项满足。
,B项满足。
因此,选择B选项。
4.基期平均数,首先题干出现“均,每,”等关键词,其次问的是过去的时间,我们称之为基期平均数问题,基期平均数与基期比重公式相同,计算方式也相同,区别在于基期平均数求得是过去时间的平均数,是一个具体的值,而基期比重则是百分数的形式。
基期平均数:基期平均数=![]()
【例】2017年全国共有各级各类民办学校17.76万所,占全国学校总数34.57%;各类民办教育在校生达5120.47万人,比上年增长6.12%。其中:民办幼儿园16.04万所,比上年增长4.00%;在园儿童2572.34万人,比上年增长5.53%。民办普通小学6107所,比上年增长2.21%;在校生814.17万人,比上年增长7.65%。民办初中5277所,比上年增长3.78%;在校生577.68万人,比上年增长8.42%。民办普通高中3002所,比上年增长7.71%;在校生306.26万人,比上年增长9.74%。民办中等职业学校2069所,比上年下降2.17%;在校生197.33万人,比上年增长7.16%。
2016年平均每所民办中等职业学校在校生人数约为:
A.871人
B.991人
C.1091人
D.1181人
【答案】A
【解析】
第一步,本题考查基期平均数计算问题。
第二步,定位文字材料,“2017年民办中等职业学校2069所,比上年下降2.17%,在校生197.33万人,比上年增长7.16%”。
第三步,根据基期平均数公式![]() ,选项未出现首位相同量级不同的情况,无需换算单位,复杂计算,可将部分数据截位处理,代入数据可得,
,选项未出现首位相同量级不同的情况,无需换算单位,复杂计算,可将部分数据截位处理,代入数据可得,![]() ,左半部分直除首两位为95,实际应为950多人,右半部分是一个小于1的数,故乘积必然小于950人。
,左半部分直除首两位为95,实际应为950多人,右半部分是一个小于1的数,故乘积必然小于950人。
因此,选择A选项。
5.基期倍数,一般题型问法是A是B的多少倍,时间是过去的时间
基期倍数:基期倍数=![]()
【例】2018年全国农产品网络零售额达2305亿元,比全国网络零售额同比增速低9.9个百分点。其中,休闲食品、茶叶、滋补食品零售额排名前三,占比分别为24.2%、12.5%和12.0%,同比增速分别为30.5%、32.5%和29.0%。
1. 2017年全国农产品网络零售品类中,休闲食品零售额约是滋补食品的:
A.1.7倍
B.2倍
C.2.3倍
D.2.6倍
【答案】A
【解析】
第一步,本题考查基期倍数计算。
第二步,定位第三段,“2018年,休闲食品、茶叶、滋补食品零售额排名前三,占比分别为24.2%、12.5%和12.0%,同比增速分别为30.5%、32.5%和29.0%”。
第三步,根据部分量=整体量×比重,当整体量(全国农产品网络零售额)一致时,可以用比重代替部分量,根据基期倍数公式,基期倍数![]() =,可得
=,可得![]() (倍),因此,选择B选项。
(倍),因此,选择B选项。










